This week, I have been measuring. This sounds as though I have been holding up a ruler to measure how high my plants have grown, or perhaps putting a dozen leaves on a balance. But no, I am using a computer to measure features of images I captured during the summer at MBL. This measuring is happening in my office or at home (when I remember to bring back the external hard drive with the 280 gigabytes worth of images); does it count as ‘lab work’? I was skeptical, but Laura convinced me that although not accomplished physically in a lab, the measurement act it is part of the experimental package and hence fair game. And game that, as this post vouchsafes, I will shoot at.

Most of my project this past summer at MBL focused on optics. But I decided that before leaving I should do one biological experiment. I decided so even while realizing that do the experiment properly I should wait until all those optics issues get resolved. Who knows when that will happen? And there is that old saying about not letting perfect be the enemy of done. I decided that I would learn things from even an imperfect experiment.

I wanted to see what happens to the cell wall after the cell has lost its microtubules. In this condition, the cell has difficulty orienting cellulose. Eri Kamon in my lab has shown for BY-2 cells that, without microtubules, the quantity of cellulose synthesized is essentially unchanged. Instead the organization of the cellulose changes. But how does it change? That is what I would like to learn. And not abandoning the optical issues, I continue to want to compare birefringence and polarized fluorescence.

Here is a brief account of the experiment from the end of July (more details here). I set up two small flasks of BY2 cells, into one of which I added a compound, propyzamide, that depolymerizes microtubules. I removed cells from each culture for imaging after 1, 2, and 3 days. Even by the second day, most of the cells without microtubules were spherical, a consequence of the altered cellulose organization. On each day, I stained the cells with fast scarlet and imaged them in both birefringence and polarized fluorescence.

These “images” are in fact image stacks. The microscope captures four or five raw images and then uses these images to calculate additional images. Thus, the saved “image” is a stack of seven or eight images. For birefringence, the calculated images show birefringent retardation (which I will refer to from here on as simply ‘retardation’) and azimuth. Retardance is a measure of the crystallinity of the object. In the calculated image, the retardation is proportional to the intensity of the pixel; thus the crystallinity at each pixel in the object is known. Azimuth is the angle the optical axis of the crystal makes with respect to a set reference direction (usually horizontal); in other words, azimuth shows which way the crystal is lined up. And again, this is calculated at each pixel. For polarized fluorescence, the calculated images show anisotropy and azimuth. Here, anisotropy refers to the degree of polarization of the fluorescence: that is, how much more fluorescence is emitted with excitation at the best angle compared to the worst angle (i.e., 90? to the best angle). And azimuth gives that best angle.

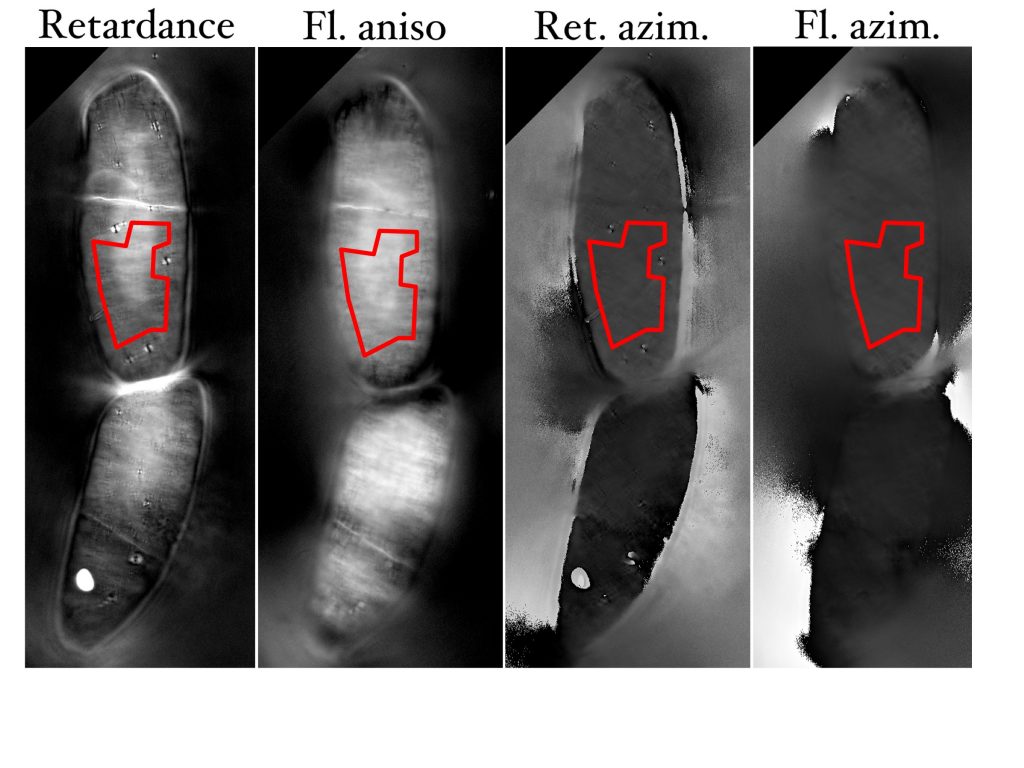
The measurement routine goes like this. I open the two stacks, one with retardation and the other with polarized fluorescence. I start with a promising cell and carefully adjust the focal plane. Oh yes, each seven or eight images in a stack (as described above) is associated with one focal plane; but, the stored stacks have a series of focal planes, making the thing a stack of stacks. If the cells were regular cylinders, then a certain focal plane would contain a nice regular swath of the cell wall; but the cells undulate. That is why I captured multiple focal planes, working my way through one side of the cell to have enough ‘flat, in-focus’ areas of wall to measure. For measuring, I draw a region of interest (an irregular polygon) defining the area of wall that I want to measure (Fig. 1). I hit ‘m’, an action that deposits parameters of my choosing in to a data window (more about these parameters in a minute). Then I shift the stack slice to azimuth. Happily the polygon comes too and hitting ‘m’ records parameters for that image. Now I have to copy the polygon to the other stack. Very happily, ImageJ has a command letting me do just that. Because the stacks represent different microscope conditions, the cells are sometimes slightly moved between retardance and fluorescence modes. In that case, I have to move the copied polygon on stack two to come as close as possible to the position it had in stack one. Then ‘m’ writes the parameters, and shifting to the azimuth slice lets me get those too. Thus, for each cell, represented by a polygon, I have four sets of measurements: retardation, retardation azimuth, anisotropy, and anisotropy orientation.

OK, so what parameters did I measure? The first one is area of the polygon. I don’t really give a hoot how big it is, but writing the area in to the window is a boon for keeping track of the data. Also will be reasonable to have a record of the sizes of all the measured regions, just in case. The second parameter is average intensity. That number is key, it will give me the retardation and anisotropy values, as well the azimuths. This just requires multiplying the pixel intensities by the appropriate proportionality factors. I decided to save one more parameter: the standard deviation of the intensity. With this, I can see how regular the region is: are all its pixels similar in intensity (low standard deviation) or do they vary (high deviation). I suspect they will vary more when microtubules are absent.

I have about 80 ‘stack of stacks’ each with several cells and focal planes. So there is a lot of slogging thru this business measuring all of those regions. It has kept me off the streets for more than one afternoon. Next time: results! Stay tuned.