Month: February 2012

The question underlying pattern formation theory is how a complex shape emerges under featureless forces and constraints. The basic paradigm here relies on a fundamental principle in modern condensed matter theory: A spontaneous breaking of continuos symmetry.

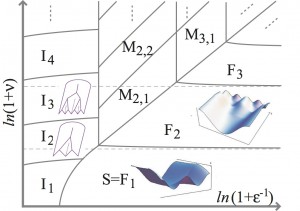In a previous work we employed this concept to address the origins for morphological complexity in thin sheets through a primary example of  simple-yet-complex shape: The “elastic curtain”. An illustration of the system is in the top figure. The basic question here is how the typical hierarchical (multi-scale) shape of curtains (e.g. in your shower) emerges spontaneously by confining one edge (the curtain rod, x=0 in the figure).  A central result of our analysis is the prediction of a novel series of elastic “period fissioning” instabilities, that govern the pattern when sufficiently large tension is exerted (along x). Furthermore, this analysis led us to conjecture the existence of a surprisingly rich phase diagram for this problem (bottom figure), in which all patterns are classified according to two parameters: A mechanical one (epsilon – the compression-to-tension ratio), and a geometric one (nu  –  the wavelength contrast along the tension direction). Later on, these parameters were recognized as particular realization of universal morphologically-relevant parameters, termed bendability, confinement, and substrate-stiffness (work in progress). In this phase diagram for the curtain problem, the predicted phases consist of hierarchical patterns of distinct types:  Smooth “period fissioning” cascades, with n generations of wrinkles (F_n), “Irregular” shapes, composed of k generations of sharp folds (I_k), and “Mixed” patterns, in which n generations of smooth wrinkles “coexist” with k generations of sharp folds (M_n,k).

This work, by Benny Davidovitch, was published in Phys.Rev.E. 80 025202 (2009).

It was inspired by (and provided the theoretical basis for) the analysis of smooth cascades of floating ultrathin sheets – an experiment by our colleagues at UMass, Amherst.

Of interest is also a recent experimental paper on the universal nature of the curtain problem by a group of researchers from Mons, Paris, MIT and Riverside.

How does one make a rippled sheet terminate at a straight edge? If the sheet is sufficiently thin, such as a piece of paper or fabric, then the obvious solution of stretching it out flat will induce large stresses near the edge, possibly even tearing the sheet apart. A solution to this problem is suggested by the series of tiny folds of fabric generated near a curtain rod. A study of wrinkling patterns on an ultrathin floating raft of polystyrene led to the discovery of a new mechanism by which nature resolves such a conflict. Rather than the hierarchy of pleats seen in curtains, a smooth cascade of ever-smaller wrinkles emerges as the edge is approached. This kind of hierarchical geometry is theoretically explained by the action of the surface tension of water that tends to “iron out” any sharp features in the sheet.  Similar types of smooth cascades may appear in other problems in materials science where a patterned surface comes up against an edge that is incompatible with the pattern.

This work, by J. Huang, B. Davidovitch, C. Santangelo, T. Russell, and N. Menon, was published in Phys. Rev. Lett. 105, 038302 (2010).

It was also featured in Physics, and in various other journals of popular science (e.g. 1, 2, and 3).

 

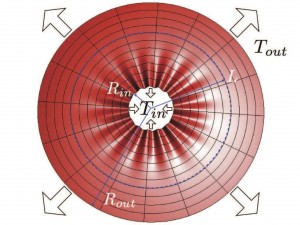
Wrinkling patterns are ubiquitous in elastic sheets of various types: plastic wraps, metallic foils, human skins, or plant leaves. Yet, the strong dependence of these patterns on physical parameters, such as the thickness of the sheet and the stretching forces, has not been well understood. In a recent theoretical work we addressed this problem. Focusing on the “simplest yet nontrivial” set-up that gives rise to wrinkles of finite size(top figure), we identified  generic parameters – termed bendability and confinement, that determine how various features of the wrinkled zone vary in a stretched sheet (phasediagram, bottom figure). The  methodology developed in this study could be used to understand wrinkling and other morphological types in simple and complex geometries.

The cusp topography of a crumpled paper appears markedly different from a smooth wrinkled skin. Nevertheless, a work that was published recently in Phys.Rev.Lett. suggests that both morphologies may simply reflect different coexistence forms between a few common “elastic building blocks”. These elementary shapes can be classified into two types: “diffuse-stress” (e.g. smooth wrinkles) and “focused-stress” (e.g. sharp folds). They have been known so far to appear, separately, under certain conditions. However, when an elastic sheet was simulated under rather general confinement, that mimic the behavior of simple curtain shape, the emerging pattern decomposed spontaneously into separate regions, each of them dominated by an elementary shape of another type. This finding may hint on a fascinating direction – rather than solving a complicated set of equations, one may construct many shapes by joining together building blocks of various types, as if they were Lego bricks. It remains to be seen whether such formalism does indeed capture the variety of patterns on thin sheets.

 The paper, by Robert D. Schroll, Eleni Katifori and Benny Davidovitch, was published in Phys.Rev.Lett. 106, 074301 (2011).

It was the subject of Physics Focus and was featured on the journal cover.

A commentary “Discretizing Wrinkling”(by Eran Sharon) was published in the Journal Club for Condensed Matter Physics.