Entanglement, Chaos & Topology
Entanglement is one of the most counterintuitive and “spooky” features of quantum mechanics. The information theoretic perspective of quantum entanglement entropy has proven an increasingly useful tool to understand and classify quantum phases of matter, and it has already revolutionized our understanding of the equilibrium properties of strongly-interacting quantum systems. Quantum information promises to do the same for non-equilibrium quantum dynamics. I am broadly interested in entanglement properties of many-body quantum systems, both at zero temperature and in non-equilibrium settings. This includes the study of topological phases of matter that have a long-range pattern of entanglement, and quantum phase transitions between distinct topological phases. Recently, I have also been interested in the “geometry” of quantum entanglement, tensor networks, and “entanglement phase transitions” where entanglement changes abruptly at a critical point.
- Review on random quantum circuits: Book chapter “Entanglement dynamics in hybrid quantum circuits” with Drew Potter (UBC) published in book “Entanglement in spin chains, from theory to quantum technology applications”.
Entanglement phase transitions and measurement-induced criticality
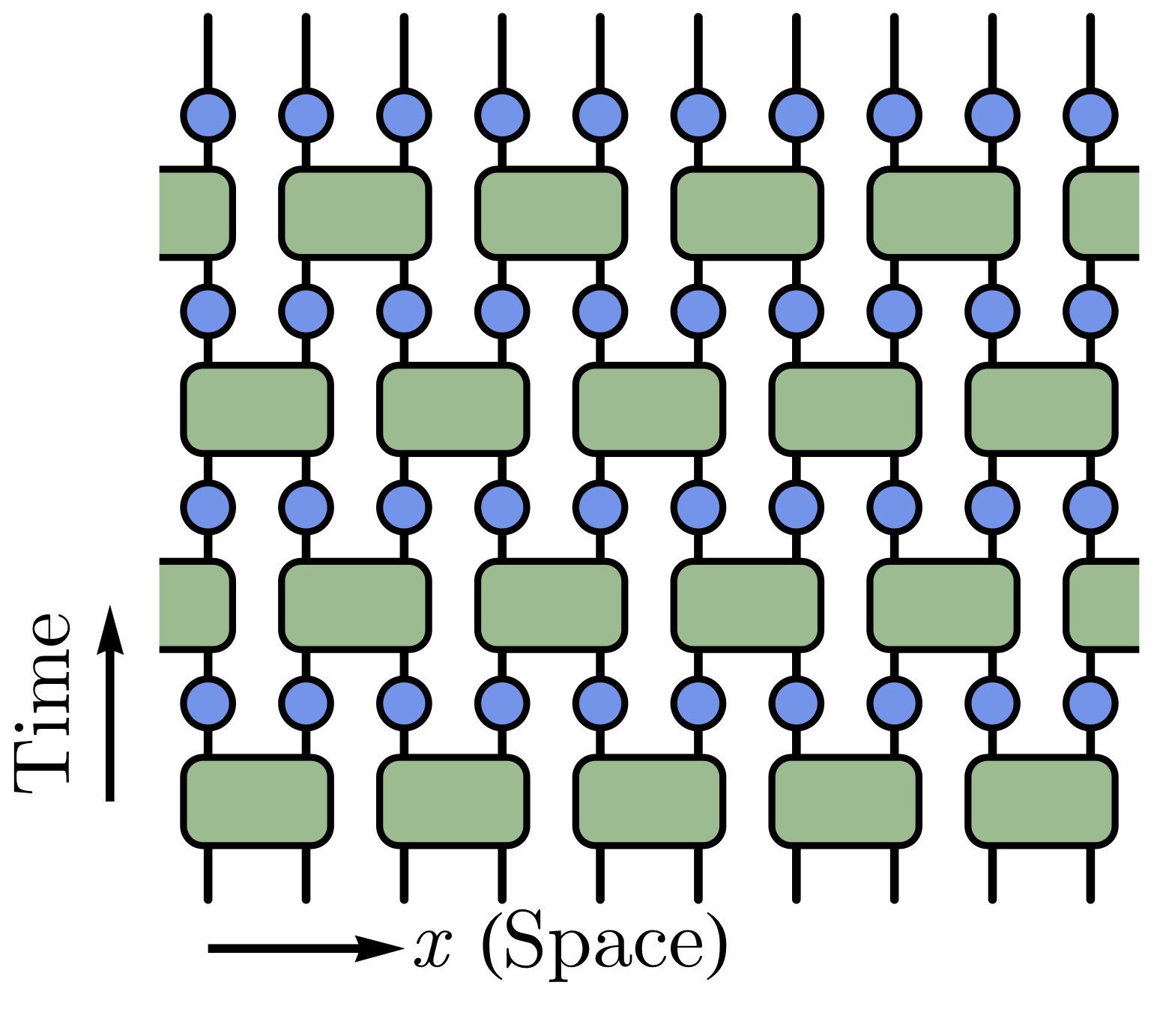
The central philosophy of statistical mechanics (stat-mech) and random-matrix theory of complex systems is that while individual instances are essentially intractable to simulate, the statistical properties of random ensembles obey simple universal “laws”. This same philosophy promises powerful methods for studying the dynamics of quantum information in ideal and noisy quantum circuits – for which classical description of individual circuits is expected to be generically intractable. We explored this idea to study the dynamics of monitored random circuits, which can loosely be thought of as noisy dynamics arising from an environment monitoring the system, and exhibit new types of measurement-induced phases and criticality. Our stat mech approach allows us to derive the general scaling properties of the entanglement entropies and mutual information near the transition using conformal invariance, and provides an analytic handle on the field theory of these entanglement transitions.
- Measurement-induced criticality in random quantum circuits, C-M. Jian, Y-Z. You, R. Vasseur and A.W.W. Ludwig, Phys. Rev. B 101, 104302 (2020).
- Measurements make the phase, B. Ware and R. Vasseur, Nature Physics 17, 298–299 (2021).
- Operator scaling dimensions and multifractality at measurement-induced transitions, A. Zabalo, M.J. Gullans, J.H. Wilson, R. Vasseur, A.W.W. Ludwig, S. Gopalakrishnan, David A. Huse & J.H. Pixley, Phys. Rev. Lett. 128, 050602 (2022).
- Triviality of quantum trajectories close to a directed percolation transition, Lorenzo Piroli, Yaodong Li, R. Vasseur & A. Nahum, Phys. Rev. B 107, 224303 (2023).
- Infinite-randomness criticality in monitored quantum dynamics with static disorder, A. Zabalo, J.H. Wilson, M.J. Gullans, R. Vasseur, S. Gopalakrishnan, D.A. Huse, and J. H. Pixley, Phys. Rev. B 107, L220204 (2023).
- Measurement induced criticality in quasi periodic modulated random hybrid circuits, Shkolnik, A. Zabalo, R. Vasseur, D.A. Huse, J.H. Pixley & S. Gazit, Phys. Rev. B 108, 184204 (2023).
- Boundary transfer matrix spectrum of measurement-induced transitions, A. Kumar, K. Aziz, A. Chakraborty, A.W.W. Ludwig, S. Gopalakrishnan, J.H. Pixley & R. Vasseur, Phys. Rev. B 109, 014303 (2024).
- Universal structure of measurement-induced information in many-body ground states, Z. Cheng, R. Wen, S. Gopalakrishnan, R. Vasseur & A.C. Potter, Phys. Rev. B 109, 195128 (2024).
- Statistical mechanics model for Clifford tensor networks and monitored quantum circuits,Y. Li, M.P.A. Fisher, R. Vasseur & A.W.W. Ludwig, Phys. Rev B 109, 174307 (2024).
Random tensor networks and complexity transitions
My collaborators and I introduced a novel class of phase transitions that we dubbed “entanglement phase transitions” separating quantum states with different entanglement features. In the spirit of random matrix theory, we introduced a simple model for such transitions where a physical quantum many-body system lives at the “holographic” boundary of a bulk random tensor network. Using a replica trick approach, we map the calculation of the entanglement properties of the boundary system onto the free energy cost of fluctuating domain walls in a classical statistical mechanics model. This provides a natural interpretation of entanglement transitions as ordering transitions in this statistical mechanics model. There transitions have a natural interpretation in terms of the complexity of contracting the tensor networks. Using mappings onto statistical mapping models, we argued that PEPS contractions corresponding to local correlators are “easy”, whereas non-local overlaps are hard to compute classically.
- Entanglement transitions from holographic random tensor networks, R. Vasseur, A.C. Potter, Y-Z. You and A.W.W. Ludwig, Phys. Rev. B 100, 134203 (2019).
- Mean-field entanglement transitions in random tree tensor networks, J. Lopez-Piqueres, B. Ware and R. Vasseur, Phys. Rev. B 102, 064202 (2020).
- Entanglement transitions from restricted Boltzmann machines, R. Medina, R. Vasseur, and M. Serbyn, Phys. Rev. B 104, 104205 (2021).
- Random insights into the complexity of two-dimensional tensor network calculations, S. Gonzales-Garcia, S. Sang, T.H. Hsieh, S. Boixo, G. Vidal, A.C. Potter & R. Vasseur, Phys. Rev. B 109, 235102 (2024).
Charge sharpening transitions and symmetric monitored quantum circuits
Monitored random quantum circuits (MRCs) exhibit a measurement-induced phase transition 
between area-law and volume-law entanglement scaling. We found that MRCs with a conserved charge additionally exhibit two distinct volume-law entangled phases that cannot be characterized by equilibrium notions of symmetry-breaking or topological order, but rather by the non-equilibrium dynamics and steady-state distribution of charge fluctuations. These include a charge-fuzzy phase in which charge information is rapidly scrambled leading to slowly decaying spatial fluctuations of charge in the steady state, and a charge-sharp phase in which measurements collapse quantum fluctuations of charge without destroying the volume-law entanglement of neutral degrees of freedom. We used statistical mechanics and effective field theory approaches to such charge-sharpening transitions, and related them to the efficiency of classical decoders to “learn” the global charge of quantum systems from local measurements. We implemented this protocol to observe the charge-sharpening transition experimentally in a trapped-ions quantum processor. Our group is currently working on studying monitored quantum circuits with non-Abelian symmetries.
- Entanglement and charge-sharpening transitions in U(1) symmetric monitored quantum circuits, U. Agrawal, A. Zabalo, K. Chen, J.H. Wilson, A.C. Potter, J.H. Pixley, S. Gopalakrishnan and R. Vasseur, Phys. Rev. X 12, 041002 (2022).
- Field theory of charge sharpening in symmetric monitored quantum circuits, F. Barratt, U. Agrawal, S. Gopalakrishnan, D.A. Huse, R. Vasseur & A.C. Potter, Phys. Rev. Lett. 129, 120604 (2022).
- Transitions in the learnability of global charges from local measurements, F Barratt, U. Agrawal, A.C. Potter, S. Gopalakrishnan & R. Vasseur, Phys. Rev. Lett. 129, 200602 (2022).
- Critical phase and spin sharpening in SU(2)-symmetric monitored quantum circuits,
S. Majidy, U. Agrawal, S. Gopalakrishnan, A.C. Potter, R. Vasseur & N. Yunger Halpern, Phys. Rev. B 108, 054307 (2023).
- Observing quantum measurement collapse as a learnability phase transition, U. Agrawal, J. Lopez-Piqueres, R. Vasseur, S. Gopalakrishnan and A.C. Potter, Phys. Rev. X 14, 041012 (2024).
Gapless topological phases of matter
A key realization over the past decades has been the role of topology in the understanding of quantum phases of matter. Topological phases of matter lack a conventional description in terms of a local order parameter, and they can show quantized properties and protected surface states, as exemplified by the celebrated topological insulators. Most topological phases enjoy a bulk gap which plays a crucial role in the protection of the topological properties. To go beyond the recent examples of non-interacting gapless topological materials such as Weyl semimetals, we have undertaken the study of a new class of strongly interacting quantum systems that are gapless in the bulk with topologically protected edge modes as long as certain symmetries are preserved. Despite the absence of a bulk gap, the topological edge modes in such gapless symmetry protected topological (gSPT) systems are robust to arbitrary symmetry-preserving boundary perturbations and require no fine-tuning beyond closing the bulk gap, leading to unusual surface criticality. We also found that symmetry-broken phases proximate in phase space to symmetry-protected topological phases can exhibit dynamical signatures of topological physics. This dynamical, symmetry-protected “topological” regime is characterized by anomalously long edge coherence times due to the topological decoration of quasiparticle excitations, even if the underlying zero-temperature ground state is in a nontopological, symmetry-broken state. Recently, I have also been working on deconfinement topological phase transitions in disordered gauge theories, and on symmetry-enriched quantum critical points and phases in disordered systems.
- Gapless Symmetry Protected Topological Order, T. Scaffidi, D.E. Parker and R. Vasseur, Phys. Rev. X 7, 041048 (2017).
- Topological Luttinger Liquids from Decorated Domain Walls, D.E. Parker, T. Scaffidi & R. Vasseur, Phys. Rev. B 97, 165114 (2018).
- Topologically Protected Long Edge Coherence Times in Symmetry-Broken Phases, Daniel E. Parker, Romain Vasseur, and Thomas Scaffidi, Phys. Rev. Lett. 122, 240605 (2019).
- Superuniversality from disorder at two-dimensional topological phase transitions, B. Kang, S.A. Parameswaran, A.C. Potter, R. Vasseur and S. Gazit, Phys. Rev. B 102, 224204 (2020).
- Topological and symmetry-enriched random quantum critical points, C.M. Duque, H.-Y. Hu, Y.-Z. You, V. Khemani, R. Verresen, and R. Vasseur, Phys. Rev. B 103, L100207 (2021).
Operator spreading and many-body quantum chaos
Operator spreading under unitary time evolution has attracted a lot of attention recently, as a way to probe many-body quantum chaos. While quantities such as out-of-time-ordered correlators (OTOC) do distinguish interacting from non-interacting systems, it has remained unclear to what extent they can truly diagnose chaotic versus integrable dynamics in many-body quantum systems. We proposed a quasiparticle picture of operator spreading in integrable systems, and showed that the operator front broadens diffusively in both integrable and chaotic interacting spin chains. We also argued that the scaling of the height of the front in integrable systems is anomalous, providing a clear though rather subtle signature of many-body quantum chaos in the operator front. More recently, we’ve been studying signatures of many-body quantum chaos and their relations to transport in kinetically constrained systems.
- Hydrodynamics of operator spreading and quasiparticle diffusion in interacting integrable systems, Sarang Gopalakrishnan, David A. Huse, Vedika Khemani, and Romain Vasseur, Phys. Rev B 98, 220303(R) (2018).
- Operator front broadening in integrable and chaotic quantum chains, J. Lopez-Piqueres, B. Ware, S. Gopalakrishnan and R. Vasseur, Phys. Rev. B 104, 104307 (2021).
- Subdiffusion and many-body quantum chaos with kinetic constraints, H. Singh, B. Ware, R. Vasseur & A. Friedman, Phys. Rev. Lett. 127, 230602 (2021).
Quantum impurities and Entanglement
The study of two metallic leads (Fermi or Luttinger liquids) connected by some sort of quantum impurity has become paradigmatic in modern quantum physics. It plays a particularly important role in the context of local quenches, transport through quantum dots, and the dynamics of magnetic impurities. An essential feature of these systems is the existence of crossover scales, which play a role similar to the Kondo temperature in the Kondo problem (a magnetic impurity in a Fermi sea), and qualitatively separate weak and strong coupling regimes. Using a strategy based on the integrable structure of the quantum field theories describing the low-energy physics of such quantum impurity problems, we were able to compute non-perturbatively the scaling of the entanglement entropy along this Kondo crossover. We also proposed an exact formula for overlaps (matrix elements) in the Kondo problem. The figure shows the universal scaling form of the entanglement entropy between two quantum wires connected through a quantum dot with Kondo temperature T_B.
- Entanglement in quantum impurity problems is non perturbative, Hubert Saleur, Peter Schmitteckert and Romain Vasseur, Phys. Rev. B 88, 085413 (2013).
- Universal entanglement crossover of coupled quantum wires, R. Vasseur, J.L. Jacobsen and H. Saleur, Phys. Rev. Lett. 112, 106601 (2014).
- Exact overlaps in the Kondo problem, S.L. Lukyanov, H. Saleur, J.L. Jacobsen and R. Vasseur, Phys. Rev. Lett. 114, 080601 (2015).
Entanglement in Random quantum critical points
One of the most basic questions about quantum dynamics is the response of a system to a sudden change of the Hamiltonian in a small region in space. An early experimental example of a “local quantum quench” from solid-state physics is the excitation of a core level by an incident photon of high energy, which appears to the conduction electrons as a sudden change in the local electrostatic potential. This led to the development of important concepts in many-body theory such as that of an orthogonality catastrophe, which is a decay with system size in the overlap of ground states of the initial and final Hamiltonians. We studied the response to a local perturbation of random (disordered) spin chains, and showed that, surprisingly, they exhibit a power-law orthogonality catastrophe similar to that in metals, even though the system is insulating. The entanglement structure of the groundstate wave function around the local perturbation shows a universal crossover that is similar to that in Luttinger liquids.